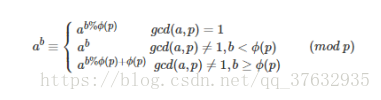数论初探
简单的数论问题
质数
埃氏筛
1
2
3
4
5
6
7
8
9
10
11
12
13
const int N = 100000 + 5;
bool prime[N];
void init(){ // 近似线性,复杂度O(nloglogn),也已经很小了
for(int i = 2; i < N; i ++)
prime[i] = true;
for(int i = 2; i*i < N; i ++){ // 注意i*i<N可以减少一多半的运算量
if(prime[i]){
for(int j = i*i; j < N; j += i){ // 从i*i开始就可以了
prime[j] = false;
}
}
}
}
欧拉筛
1
2
3
4
5
6
7
8
9
10
11
12
13
14
const int N = 100000 + 5;
bool prime[N];//prime[i]表示i是不是质数
int p[N], tot;//p[N]用来存质数
void init(){ // 线性筛,每个数只会被筛掉一次
for(int i = 2; i < N; i ++)
prime[i] = true;//初始化为质数
for(int i = 2; i < N; i++){
if(prime[i]) p[tot ++] = i;//把质数存起来
for(int j = 0; j < tot && i * p[j] < N; j++){
prime[i * p[j]] = false;
if(i % p[j] == 0) break;//保证每个合数被它最小的质因数筛去
}
}
}
每个数的质因数分解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const int N = 100000 + 5;
vector<int > prime_factor[N];
void init(){
int temp;
for(int i = 2; i < N; i ++){
if(prime_factor[i].size() == 0){
for(int j = i; j < N; j += i){
temp = j;
while(temp % i == 0){
prime_factor[j].push_back(i);
temp /= i;
}
}
}
}
}
快速乘&快速幂
1
2
3
4
5
6
7
8
9
LL pow_mod(LL a, LL b, LL p){ // a^b%p
LL ret = 1;
while(b){
if(b & 1) ret = (ret * a) % p;
a = (a * a) % p;
b >>= 1;
}
return ret;
}
1
2
3
4
5
6
7
8
9
LL mul(LL a, LL b, LL p){ // 快速乘,计算a*b%p
LL ret = 0;
while(b){
if(b & 1) ret = (ret + a) % p;
a = (a + a) % p;
b >>= 1;
}
return ret;
}
欧拉降幂求快速幂
欧拉定理
\[a^{\phi(n)}\equiv 1(\mod n)\]有降幂公式
第一个要求a和p互质,第二个和第三个是广义欧拉降幂,不要求a和p互质,但要求b和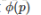
广义欧拉降幂能够处理的范围近乎是无穷大,分为两种情况,
一种是b<phi(p) ,这种情况直接调用快速幂即可 .
另一种就是我们所关心的情况了,按照公式计算即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
ll phi(ll n) { // 求欧拉函数值,类似求质因数分解,因为此处主要是对于mod求,实际上还能优化(只需要一次运算,之后直接读取即可)
ll ans=n,temp=n;
for(int i=2; i*i<=temp; i++) {
if(temp%i==0) {
ans-=ans/i;
while(temp%i== 0)
temp/=i;
}
}
if(temp>1)
ans-=ans/temp;
return ans;
}
ll mod_pow(ll x,ll n,ll mod) { // 快速幂,常见操作
ll ans=1;
while(n) {
if(n%2==1)
ans=ans*x%mod;
x=x*x%mod;
n/=2;
}
return ans;
}
char b[10000500]; // b的大小取决于输入范围的大小
while(scanf("%s",b)!=EOF) { // 为了简化问题,此处仅仅输入b
ll phic=phi(mod); // 在模数固定的情况下,可以将它提到主函数外面,以加快运行速度
ll i,len=strlen(b);
ll res=0,ans;
for(i=0; i<len; i++) {
res=res*10+b[i]-'0';
if(res > phic)
break;
}
if(i==len) { // 情况1
/*
直接快速幂
*/
ans = mod_pow(a,res,mod)%mod;
} else { // 情况2
res=0;
for(int i=0; i<len; i++) {
res=res*10+b[i]-'0';
res%=phic;
}
// res 即 b%phic
ans = mod_pow(a,res+phic,mod)%mod; // ans = a^( b%phic + phic )
}
printf("%lld\n",ans);
}
lowbit()
1
2
3
int lowbit(int x){ // 用于获取某个数字的二进制表示的最后一位'1'所对应的值
return x&(-x);
}
首先,1byte=8bit,c++中的int类型是4字节,也就是32位二进制。
然后这里再温习一下关于数字在内存中表示的问题
- 计算机系统中,数值一律用补码来表示和存储
- 正数的补码是其二进制表示,和原码相同
- 负数的补码,将其原码除符号位外的所有位取反,然后加1.
- 若已知负数绝对值的原码,则将此原码所有位取反+1得到的就是此负数的补码
至于转换成原码:
- 若第一位是’0’,则表示其是一个正数,其原码就是补码
- 若第一位是‘1’,则表示其是一个负数,那么这个补码的补码就是要求的原码
回到此函数,我们采取一个例子来印证
x = ????1000 ,根据负数的补码需绝对值按位取反+1可知,-x=????0111+1=????1000(问号部分我们不研究)
即最后一个1变成了0,后面的’0’也全部化成了’1’,然后在+1 的过程中后面的’1‘又都变成了’0’,而这个位又变回了’1’,而此位之前的所有位置都与原数相反。
故 x&(-x)=1000,即返回某个数字二进制所代表的值
求某数二进制1的个数
lowbit法
因此可以衍生出函数用以求某个数二进制形式的’1‘的个数
1
2
3
4
5
6
7
8
int Cnt(int x){ // x的二进制表示中有多少个'1'
int res=0;
while(x){
x -= lowbit(x);
res++;
}
return res;
}
__builtin_popcount
然后我就发现了一个更加奇葩的办法,GCC里面居然有__builtin_popcount(unsigned u) 的函数,其直接返回二进制1的个数,其内部原理应该是查表,但是我感觉太过技巧性,还是少用为妙
n&(n-1)
先上代码
1
2
3
4
5
6
7
8
int Cnt(int x){ // x的二进制表示中有多少个'1'
int res=0;
while(x){
x &= (x-1);
res++;
}
return res;
}
这个方法的证明也很简单,还是假设x=10001000,那么x-1=10000111,则不难发现,x&(x-1)得到的结果只会将x的最后一个1变成0,而对x的前面没有影响,故有多少个1,这个操作就可以执行多少次,执行到最后的结果是x变成0
平方和
- 四平方和定理:每个正整数都可以表示成四个整数的平方数之和。在这个定理中,四个整数中可以有为0的。
- 正整数n能表示为三个数的平方和的充要条件是n不可以表示为
的形式,其中m,k为非负整数。(如果不能表示为三个整数平方和,那么也就不能表示为两个数的平方和 )
- 每一个大于等于170的整数n,都可以表示为五个正整数的平方和。
故判断一个数最少能用几个正整数的平方和表示,可使用如下代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
typedef long long LL;
int Solve(LL n) { // 有点玄学
int i,k;
LL tmp;
while(n%4==0) n>>=2; //先消去所有4的因数
if(n%8==7) return 4; //如果不能表示为三个整数平方和,那么也就不能表示为两个数的平方和
for(i=8,tmp=9;tmp<=n;i+=8,tmp+=i) //消去所有素因子的偶次幂
while(n%tmp==0)
n/=tmp;
if(n==1)
return 1;
if(n%2==0)
n>>=1;
if(n%4==3)
return 3;
for(k=sqrt(n),i=3;i<=k&&n%i;i+=4);
return i>k? 2:3;
}
## GCD
常用欧几里得算法,又称辗转相除法,求模线性方程的基础.
有三个公式需要记住
- lcm = a * b / gcd
- gcd(ka, kb) = k * gcd(a, b)
- lcm(ka, kb) = k * lcm(a, b)
可以推出一个很有意思的公式,令(2)中的k=1/(ab),代入得gcd(1/a,1/b) = gcd(a,b)/(a,b),代入(1)得,gcd(1/a,1/b) = 1/lcm(a,b)
1
2
3
int gcd(int a, int b){ // 辗转相除法求最大公约数(当然参数及返回值换成long long 也没有关系)
return b ? gcd(b, a % b) : a;
}
扩展欧几里得算法
这个算法是基于欧几里得算法而来的,用以解决ax+by = gcd(a, b)形式的线性方程(根据裴蜀定理,此方程一定有解,在此不再证明)
1
2
3
4
5
6
7
8
9
10
11
12
int exGcd(int a,int b,int &x,int &y){
if(b==0){
x=1;
y=0;
return a;
}
int r=exGcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
return r;
}
然而如果仅仅是这样的话,其适用范围很小,但是我们可以用其求ax+by=c这种更具普遍意义的方程.
ax+by=c
首先,当且仅当 c%gcd(a,b)==0时有解,且令x=k*m,y=k*n,c=k*gcd(a,b) ,则可令上式改写成am+bn == gcd(a,b) ,解出 M0,N0,令X0 = k*M0 = c*m/gcd(a,b) Y0 = k*N0 = c*n/gcd(a,b)
然后就有 X = X0 - b/gcd(a,b)*t Y = Y0 + a/gcd(a,b)*t
也就是X = (c*M0 - b*t)/gcd(a,b) Y = (c*N0 + a*t)/gcd(a,b)
(t 是任意一个整数)
若此题要求X,Y的最小正整数解,则有公式:(此处太过复杂且方法不一,采取最保险的方式)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
while (cin >> x >> y >> m >> n >> l) {
ll a = n - m;
if (!a) {
cout << "Impossible" << endl;
continue;
}
ll X0, Y0;
ll d = ex_gcd(n - m, l, X0, Y0);
ll r = l / d;
if ((x - y) % d) {
cout << "Impossible" << endl;
continue;
} else {
// 求 (n-m)*X + l*Y = x-y
// 令 a = n-m
// 令 b = l
// 令 r = b/gcd(a,b)
// 令 c = x-y
// aX + bY = c (1)
// 即 aX = c(mod b) 的解
// 扩展欧几里得算法求的是 ax+by = gcd(a,b) 的解,令(1)式左右同除gcd(a,b)
// 得 a/gcd(a,b) * X + b/gcd(a,b) *Y = c/gcd(a,b)
// 令 a'X+b'Y=c' 代替上式
// 再 令 x0=X/c' y0=Y/c'
// 得 a'x0+b'y0=1
// 式中a' b' 互质,即gcd(a',b')=1,满足扩展欧几里得所需条件
// 因此用扩展欧几里得算法可以求出x0,y0
// 又 有 X = x0*c' Y = y0*c' ,所以能求出X,Y
// 但是回到题目发现这只是特解,
// 实际上 X = x0*c' + b'*t = x0*c/gcd(a,b) +b/gcd(a,b)*t = (x-y)/gcd(a,b)*x0 + l/gcd(a,b)/gcd(a.b)*t
// Y = y0*c' - a*t ( t=0,1,...)
// 此处要求最小正整数解,所以 X = (c/gcd(a,b)*x0%r+r)%r
// 若求Y,则为 Y = (c/gcd(a,b)*y0%r+r)%r
cout << ((x - y) / d * X0 % r + r) % r << endl;
}
以上废话有点多,说白了
-
得到
ax+by=c, 等价于ax=c (mod b) -
求
a*X0+b*Y0= gcd(a,b)的解 X0,Y0 -
令
r = b/gcd(a,b) -
得到最小整数
X = (c/gcd(a,b)*x0%r+r)%r - 得到最小整数
Y = (c/gcd(a,b)*y0%r+r)%r
逆元
对于加减乘除,我们不难发现,其在模意义下
(a + b) % p = (a%p + b%p) %p (对)
(a - b) % p = (a%p - b%p) %p (对)
(a * b) % p = (a%p * b%p) %p (对)
(a / b) % p = (a%p / b%p) %p (错)
除法的错误是显然的,举例子(100/50)%20 = 2 ≠ (100%20) / (50%20) %20 = 0
定义
我们定义逆元(数论倒数)如下,a*x = 1 (mod p),则x是a关于p的逆元,比如2*3%5==1,则称3是2关于5的逆元,或者是2和3关于5互为逆元,a的逆元我们用inv(a)来表示
有了逆元之后,我们就可以将除法转换成乘法(a/b)%p = (a*inv(b))%p=((a%p)*(inv(b)%p))%p,但切记a和p互质才有逆元.
计算
暴力
这个很显然,直接疯狂暴力穷举即可.
1
2
3
4
5
6
7
int n;
for(int i = 1 ;i <= P ;i++){ // 复杂度O(P),无需在乎P是否是素数
if(x * i % P == 1){
n = i;
break;
}
}
费马小定理+快速幂
这个要求P是质数 ,根据费马小定理
假如p是质数,且gcd(a,p)=1,那么 a^(p-1)≡1(mod p)
我们对此式稍作变形,得 a*a^(p-2)≡1(mod p),也就是 a^(p-2)%p是a的逆元
这一步直接快速幂就可得答案了.复杂度O(log P)
欧拉定理+快速幂
不要求p是质数
a^phi(p)=1(mod p), 式中phi为欧拉函数
由费马小定理求逆元的过程可知,a^(phi(p)-1)%p 是a关于p的逆元,但是需要预处理欧拉函数
扩展欧几里得算法
给定模数n,求a的逆相当于求解ax=1(mod p),这个方程可以转化为ax+py=1,然后套用二元一次方程的方法,用扩展欧几里得算法求得一组x0,y0和gcd;
- gcd不为1说明逆元不存在
- 若为1,调整x0到0~p-1的范围中即可。
1
2
3
4
5
6
7
8
int mod_reverse(int a,int p){ // ax=1(mod n) 求a的逆元x
int d,x,y;
d=ex_gcd(a,p,x,y);
if(d==1)
return (x%p+p)%p; // 调整至0-p-1范围内
else
return -1; // a p不互质,无逆元
}
递推求逆元
有神奇的公式: inv[i]=(M-M/i)*inv[M%i]%M (其中M为模数,要求为奇质数)
设t=M/i,k=M%i,那么
t*i+k≡0(Mod M)-t*i≡k(Mod M)对上式两边同时除 i×k,进一步得到-t*inv[k]≡inv[i](Mod M)再把和替换掉,最终得到
inv[i]=(M-M/i)*inv[M%i]%M
1
2
3
4
5
6
7
void InverseElement(int n,int p){
A[1]=1;
for(int i=2;i<=n;i++) {
A[i]=(p-(p/i))*A[p%i]%p;
printf("%d %d %d\n",i,A[i],(i*A[i])%p);
}
}
唯一分解定理
定义
任何一个大于1的自然数N,如果N不是质数,那么N可以分解成有限个素数的乘积.如果不计顺序,则这种分解是唯一的
换言之,就是N=p1^a1*p2^a2*…*pn^an,式中pi均为质数,实际上,若N是质数,则a1,a2….a(n-1)都是0,pn==N,an==1,也就是 N=N^1 ,也算是符合定义中的表述
### 应用
求质因数个数
由前文可知,质因数分解是唯一的,所以只要按照唯一分解定理从小到大逐个因子进行去除,就能得到质因子个数(还能得到其幂)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int CntPrime(int n){
int ans=0;
for(int i=0;i<tol&&prime[i]*prime[i]<=n;++i){
if(n%prime[i]==0){
int cnt=0;
while(n%prime[i]==0){
n/=prime[i];
++cnt;
}
/*
在此处就得到了 质因子 prime[i] 和 其幂 cnt,这里就可以进行很多操作了,此处以举例为目的,故仅数出来质因子个数
*/
++ans;
}
}
if(n>1){ // 注意这种情况,结合上文代码考虑,这种情况是指n排除了所有小于等于√n的因子之后,仍然还有因子的情况,可想而知,大于√n的因子绝对不超过一个,(因为两个大于√n的因子相乘其结果一定大于n),所以如果有这种因子的话,其个数一定为1(事实上此时的n就是这个因子)
++ans;
}
return ans;
}
求因数个数
质数是数字的砖块,实际上,一个数所有的因数无非是其质因数的组合,而由唯一分解定理可知,不同质因数的组合一定会出现不同的因数(否则就会出现不同质数的乘积对应同一个数的情况),因此,因数的个数=(1+a1)*(1+a2)*(1+a3)*.....*(1+an) ,仍然采用上文的框架,仅仅把++ans;替换成ans *=(1+cnt),当然,ans的初始值也要设置为1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int CntFactor(int n){
int ans=1; // 注意初始值
for(int i=0;i<tol&&prime[i]*prime[i]<=n;++i){
if(n%prime[i]==0){
int cnt=0;
while(n%prime[i]==0){
n/=prime[i];
++cnt;
}
// 以上部分都无需变动
ans *= (cnt+1);
}
}
if(n>1){ // 此种情况同上,不再赘述
ans *= (1+1); // 也就是cnt==1时候的情况
}
return ans;
}
求在0-n范围内 LCM为n的无序对数
依旧根据唯一分解定理将n分为n=p1^a1*p2^a2*...*pn^an,当然此处的所有位的指数都是正数,我们不妨设LCM(i,j)=n,则i=p1^e1*p2^e2*...*pn^en,j=p1^f1*p2^f2*...*pn^fn,而i,j最小公倍数为n,则决定了,对于任意一位K,均有max(ek,fk)=ak,而满足这种条件话,分为两种情况,
ek == ak,fk的范围是[0,ak],共ak+1种可能fk == ak,ek的范围是[0,ak],共ak+1种可能
但是这两种情况重复了两者都是ak的情况,所以对于任意一位k, 共2*ak+1种可能,也就是将所有位的可能情况相乘即达到了答案
但是,这个题要求的是无序的,因此需要将其除以二加一,有一个很有趣的事实是,无论多少个2*ak+1相乘,其结果一定是奇数,所以这里除以二加一和先加一再除以二并没有区别
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int CntLCMPair(int n){
int ans=1; // 注意初始值
for(int i=0;i<tol&&prime[i]*prime[i]<=n;++i){
if(n%prime[i]==0){
int cnt=0;
while(n%prime[i]==0){
n/=prime[i];
++cnt;
}
// 以上部分都无需变动
ans *= (2*cnt+1);
}
}
if(n>1){ // 此种情况同上,不再赘述
ans *= (2+1); // 也就是cnt==1时候的情况
}
return (ans+1)>>1;
}
全体正因数之和
全体正因数之和为(1+p1+p1^2+...+p1^a1)*(1+p2+p2^2+...+p2^a2)*...*(1+pn+pn^2+...+pn^an)
若N的全体正因数之和为2N,则称N为完全数.
这个结论也很显然,也就是穷尽质因数的所有组合,结合唯一分解定理,对于每一位穷举所有组合,然后所有位乘在一起,展开后就是所有质因数的和
积性函数
概念
- 积性函数:对于任意互质的整数a和b有性质
f(ab)=f(a)*f(b)的数论函数。 - 完全积性函数:对于任意整数a和b有性质
f(ab)=f(a)f(b)的数论函数。
举例
- φ(n) -欧拉函数
- μ(n) -莫比乌斯函数,关于非平方数的质因子数目
- gcd(n,k) -最大公因子,当k固定的情况
- d(n) -n的正因子数目
- σ(n) -n的所有正因子之和