训练联盟 第一场
日拱一卒,功不唐捐
A. 图像压缩四叉树
题目描述
四叉树把大量坐标数据压缩包存在内存空间中,它总是将给定空间分割成4个,然后以递归形式标识,故得名四叉树。其最著名的应用是对黑白图像的压缩。
四叉树会用字符串的形式对 2^N * 2 ^N的黑白图像进行如下压缩。
- 如果所有像素是黑色,无论图像大小是多少,四叉树压缩的结构都是b;
- 图像所有像素是白色,则无论图像大小是多少,四叉树压缩结果都是w;
- 图像的像素不都是相同颜色,则先把图像纵向及横向各一分为二,然后对4个小图像进行压缩。整个图像的压缩结果为x(左上部分的压缩结果)(右上部分的压缩结果)(左下部分的压缩结果)(右下部分的压缩结果)。例如,下图左上侧的压缩结果为xwwwb.
上图表示将 16 * 16的一个图。此图像的最终压缩结果为
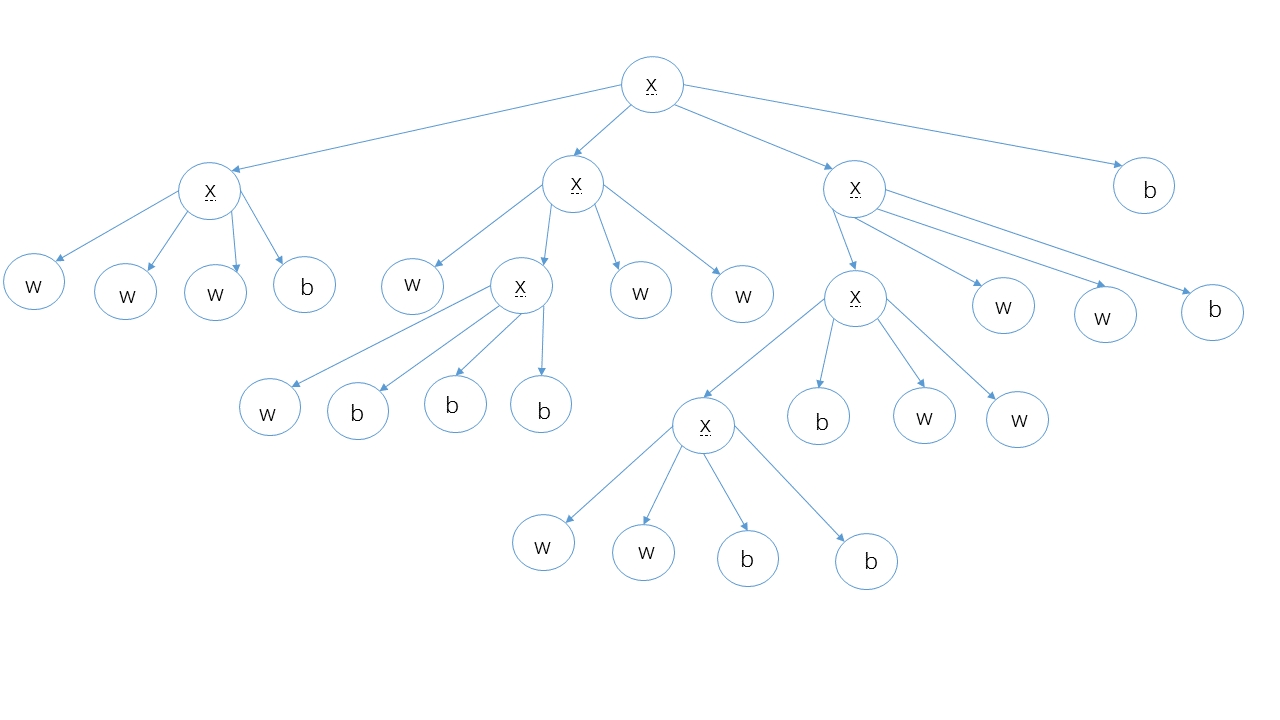
下面解决另一个四叉树问题。给定一个利用四叉树压缩过的黑白照片,对此图像进行上下翻转,然后利用四叉树算法对其进行压缩。
输入描述
第一行有一个整数 n ( 1 <= n <= 50 ) 表示测试数据的数量。
在之后的n行里,每行输入一个四叉树压缩过的图像,每行的字符串不超过10 000个字符,原图像的大小不超过 2^(20) * 2^(20)
输出描述
每一组测试数据的输出应该包含2行。
第一行表示格式为”Case #t:”表示测试数据是第t组;
第二行输出上下翻转给定图像再利用四叉树进行压缩的结果。
样例输入
1
2
3
4
5
4
w
xbwwb
xbwxwbbwb
xxwwwbxwxwbbbwwxxxwwbbbwwwwbb
样例输出
1
2
3
4
5
6
7
8
Case #1:
w
Case #2:
xwbbw
Case #3:
xxbwwbbbw
Case #4:
xxwbxwwxbbwwbwbxwbwwxwwwxbbwb
思路
这套题里面最简单的一个题.这个题就是单纯的模拟,以前写过二叉树的构建,这次是四叉树,而且到叶子节点没有提示(或者说此题提示的是非叶子节点),也算是练手了.在构建完树后,以2,3,0,1的顺序dfs输出即可
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <iostream>
#include <cstdio>
#include <cstring>
#define ll long long
#define sc scanf
#define INF (long long)(1e18)
using namespace std;
struct node {
char data;
int child[4];
} tree[10000+100];
int n;
char mp[10000+10];
int len=0;
int tot=0;
void init() {
for(int i=0; i<=len; ++i) {
for(int j=0; j<4; ++j) {
tree[i].child[j]=-1;
}
}
tot=0;
}
int build() {
int ans = tot;
++tot;
tree[ans].data=mp[ans];
if(mp[ans]=='x') { // 强迫症一本满足
tree[ans].child[0]=build();
tree[ans].child[1]=build();
tree[ans].child[2]=build();
tree[ans].child[3]=build();
}
return ans;
}
void dfs(int pos) {
printf("%c",tree[pos].data);
if(tree[pos].child[2]!=-1) {
dfs(tree[pos].child[2]);
}
if(tree[pos].child[3]!=-1) {
dfs(tree[pos].child[3]);
}
if(tree[pos].child[0]!=-1) {
dfs(tree[pos].child[0]);
}
if(tree[pos].child[1]!=-1) {
dfs(tree[pos].child[1]);
}
}
int main() {
int T;
sc("%d",&T);
int cnt=0;
while(T--) {
printf("Case #%d:\n",++cnt);
sc("%s",mp);
len = strlen(mp);
init();
build();
dfs(0);
printf("\n");
}
return 0;
}
B. 最大子串奇数和
题目描述
输入n,然后再输入n个数字,问所有子串中和为奇数的最大值是多少。保证一定有子串和为奇数,且子串中可能有负数。
注:子串是连续的串,比如1,5,3中(1,5,3),(1),(5),(3),(1,5),(5,3)是子串,而(1,3)不是。和分别为1+5+3 = 9,1,5,3,1+5=6,5+3 = 8,所以最大的奇数就是9,对应的子串为(1,5,3)。
输入描述
第一行输入T,T组数据
下面2*T行:
第i行三个数字N,(1 <= N <=1000,000)
下面i+1行:N个数字,表示所有的数。
输出描述
输出第一行:
Case #数据标号:
下一行:子串中和为奇数时的最大值。(题目保证一定有奇数出现)。
样例输入
1
2
3
1
3
1 3 5
样例输出
1
2
Case #1:
9
思路
这个题一看就是简单dp,我一开始就想到了大概的思路,但是调了很久都没有调对,在此把思路先写下来
我们首先定义数组dp[i][0] 表示 从1到i,且以a[i]为结尾的为偶数的子串和
dp[i][1] 表示 从1到i,且以a[i]为结尾的为奇数的子串和 我们最后要求的答案就是dp[n][1]
状态转移方程如下
1
2
3
4
5
6
7
8
tmp=a[i];
if(tmp%2) {
dp[i][1]=tmp+max(0ll,dp[i-1][0]);
dp[i][0]=tmp+dp[i-1][1];
} else {
dp[i][1]=tmp+dp[i-1][1];
dp[i][0]=tmp+max(0ll,dp[i-1][0]);
}
转移的正确性一目了然,就是奇偶数相加的问题,但是会带来一个问题,
我们举个例子: 如果a[1]=2,那么dp[1][1] 的值应该是什么呢?应该什么都不是,而更可怕的是如果之后的转移方程用到了这个数据,那就会导致整个程序错误.
同理,如果a[1]=1,那么dp[1][0] 的值也是未定义的,这也是一个问题.
解决方法可以参考背包九讲的”初始化问题” 只要把初始值设定为-∞,那么在状态转移的过程中,由它转移的状态也是-∞,就会在之后的转移中被0给覆盖掉.
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// https://nanti.jisuanke.com/t/16465
#include <iostream>
#include <cstdio>
#include <cstring>
#define ll long long
#define INF (long long)(1e18)
using namespace std;
ll dp[1000000+100][2];https://nanti.jisuanke.com/t/16465
int main() {
int T;
cin>>T;
int cnt=0;https://nanti.jisuanke.com/t/16465
while(T--) {
dp[1][0]=-1*INF;
dp[1][1]=-1*INF;
cout<<"Case #"<<++cnt<<":"<<endl;
int n;
cin>>n;
ll a1;
cin>>a1;
if(a1%2==0) {
dp[1][0]=a1; // 合法的初始值,此时的dp[1][1]是负无穷
} else {https://nanti.jisuanke.com/t/16465
dp[1][1]=a1;
}
for(int i=2; i<=n; ++i) {
ll tmp;
cin>>tmp;
if(tmp%2) {
dp[i][1]=tmp+max(0ll,dp[i-1][0]);
dp[i][0]=tmp+dp[i-1][1];
} else {
dp[i][1]=tmp+dp[i-1][1];
dp[i][0]=tmp+max(0ll,dp[i-1][0]);
}
}
ll maxn=dp[1][1];
for(int i=1; i<=n; ++i) {
maxn = max(maxn,dp[i][1]);
}
cout<<maxn<<endl;
}
return 0;
}
C. Destroy City(未完全理解,之后再更新)
D. n点共圆
题目描述
圆上均匀是排列n个点,其中有的点黑色的(用0表示),其余的都是白色(用1表示)。现在给定n和这些点的颜色,你需要判断是否存在一些白色点能构成一个正多边形。
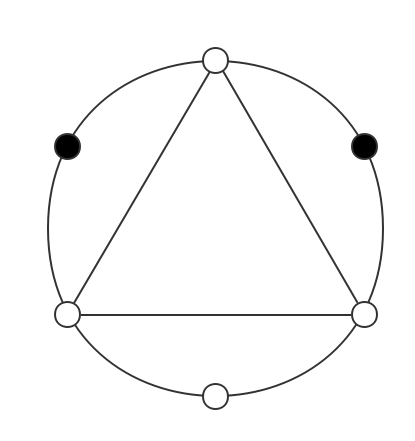
上图对应样例第二组数据
输入描述
第一行有一个整数T,表示测试数据的组数。
随后每一组数据第一行输入一个整数n,表示点的个数。第二行输入n个正整数,表示按顺时针给出的n个点的颜色。
其中
3≤n≤300000
输出描述
对于每组数据,输出一行结果。首先输出”Case #d: “,dd是当前数据的组编号。如果存在一些白色的点能构成一个正多边形,则输出”Yes”,否则,输出”No”。
样例输入
1
2
3
4
5
6
7
3
3
1 1 1
6
1 0 1 1 1 0
6
1 0 0 1 0 1
样例输出
1
2
3
Case #1: Yes
Case #2: Yes
Case #3: No
思路
显然有一个暴力算法,就是枚举n的所有因数作为分割的块数,然后依次验证,就可以了,但是求一个数所有因数的复杂度是O(√n) ,然后验证此因数合不合法的复杂度是O(n) ,总复杂度是O(n√n) ,勉强能过.
然后我们发现,我们刚才的操作其实有些繁琐,比如说,比如n==12的情况,如果它能分成三块,那么就没必要讨论能不能分成六块了,因为已经有解了;因为如果不能分成三块,就一定不能分成六块.此情况适用于所有非素数的因子,所以这就说明我们没必要遍历所有因数,只需要遍历所有质因数就可以 ,这样的话,我们就将算法复杂度降低到了将近O(logn *(logn*logn))
然后根据我们的推断发现:在3e5范围内,一个数最多有六个质因数,
1
2
3
// 2*3*5*7*11*13 == 30*77*13 == 30030
// 2*3*5*7*11*13*17 == 30*77*13*17 == 510510 > 5e5 > 3e5
// 因为最小的七个质因数都大于数据范围,故任意的n的质因数分解式子不会超过六个质因数
所以上式的复杂度可能比预想的还要低
在这一切做完之后还有一个致命的问题
题目中说多边形最少也要是3边,但是第一个质数是二,也就是绝对是不能分成两份的,但是分成4份是可以的,所以需要在打表的质数中将2改成4.
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <iostream>
#include <cstdio>
#include <cstring>
#define ll long long
#define sc scanf
#define INF (long long)(1e18)
using namespace std;
int n;
const int N = 100000 + 5;
int a[300000+100];
bool prime[N];//prime[i]表示i是不是质数
int p[N], tot;//p[N]用来存质数
void init() { // 线性筛,每个数只会被筛掉一次
for(int i = 2; i < N; i ++)
prime[i] = true;//初始化为质数
for(int i = 2; i < N; i++) {
if(prime[i])
p[tot ++] = i;//把质数存起来
for(int j = 0; j < tot && i * p[j] < N; j++) {
prime[i * p[j]] = false;
if(i % p[j] == 0)
break;//保证每个合数被它最小的质因数筛去
}
}
}
bool check(int num) { // 分成几分
// cerr<<"num == "<<num<<endl;
int step = n/num; // 一块多大
// cerr<<"step == "<<step<<endl;
for(int i=0; i<step; ++i) {
bool flag=1;
for(int j=i; j<n; j+=step) {
if(a[j]==0) {
flag=0;
break;
}
}
if(flag) {
return 1;
}
}
return 0;
}
bool CntPrime(int n) {
for(int i=0; i<tot && p[i]<=n; ++i) {
if(n%p[i]==0) {
int cnt=0;
while(n%p[i]==0) {
n/=p[i];
++cnt;
}
if(check(p[i])) {
return 1;
}
}
}
return 0;
}
int main() {
init();
p[0]=3; // 细节
p[1]=4; // 细节
int T;
sc("%d",&T);
int cnt=0;
while(T--) {
sc("%d",&n);
for(int i=0; i<n; ++i) {
sc("%d",&a[i]);
}
printf("Case #%d: ",++cnt);
if(CntPrime(n)) {
printf("Yes\n");
} else {
printf("No\n");
}
}
return 0;
}
