从KMP到AC自动机
KMP
KMP是个非常常见的算法了,但是一直没有详细总结,在此总结一下。
简介
KMP算法是用于解决这样的问题:有一个文本串S,和一个模式串P,现在要查找P在S中的位置.
我们假设S的长度是n,P的长度为m,则暴力匹配的最坏复杂度是O(n*m) ,非常爆炸。因为其中间有非常多的重复比较,所以就从这个角度着手优化。
KMP算法通过模式串自身的性质,来减少匹配的复杂度,O(n+m),近似线性的复杂度。
原理
其原理是这样的,我们假设拥有一个next数组,如果p[j]和对应位置的不匹配,那么就让p串左移至p[next[j]] 位置和当前位置,继续尝试匹配.其中next数组的含义是
代表当前字符之前的字符串中,有多大长度的相同前缀后缀。例如如果next [j] = k,代表j 之前的字符串中有最大长度为k 的相同前缀后缀。
模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
//优化过后的next 数组求法
void GetNextval(char *p, int next[]) {
int pLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < pLen - 1) {
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p[j] == p[k]) {
++j;
++k;
//较之前next数组求法,改动在下面4行
if (p[j] != p[k])
next[j] = k; //之前只有这一行
else
//因为不能出现p[j] = p[ next[j ]],所以当出现时需要继续递归,k = next[k] = next[next[k]]
next[j] = next[k];
} else {
k = next[k];
}
}
}
int KmpSearch(char *s, char *p) {
int i = 0;
int j = 0;
int sLen = strlen(s);
int pLen = strlen(p);
while (i < sLen && j < pLen) {
//①如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++
if (j == -1 || s[i] == p[j]) {
i++;
j++;
} else {
//②如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]
//next[j]即为j所对应的next值
j = next[j];
}
}
if (j == pLen)
return i - j;
else
return -1;
}
###
除此之外还有BM算法和Sunday算法,不过kmp更常用一些.
扩展kmp
介绍
扩展KMP算法是用于解决以下问题:定义母串S和子串T,S的长度为n,T的长度为m求 字符串T 与 字符串S的每一个后缀 的最长公共前缀
也就是说,设有extend数组:extend[i]表示T与S[i,n-1]的最长公共前缀,要求出所有extend[i](0<=i<n)。
为什么叫扩展kmp算法呢,是因为,如果有extend[i]=m,则说明以S[i]开头,就可以找到T的一个匹配.遍历一遍,就能找到T的所有匹配.
原理
这个算法的原理脑洞很大.我们假设自己已经求出来一个next数组(注意,这个数组和上文的next数组截然不同.)
此处的next[]数组:next[i]表示T[i,m-1]和T的最长公共前缀长度
咋看似乎莫名其妙.但是在之后的分析中会反复用到这个定义,切记切记.
首先extend[0]只能暴力计算了,没有办法.
然后假设我们已经知道了extend[0..k],准备求extend[k+1].而且,对于S来说,我们之前匹配过的最远的位置是P,(此处的匹配最远是指的i+extend[i]的最大值,也就是最远的成功匹配的下一位,取最大值时的i我们称之为P0.)
我们发现了一个问题,就是S[P0,P]=T[0,P-P0] ,这是显然的,是由extend的定义可以得出的.而且,k一定在[P0,P]之间. 但是k+1可能在区间内,也可能是P+1.
我们先假设在区间内.
此时的灰色部分表示extend数组已经完成的部分.
根据定义,我们知道S[P0,P]=T[0,P-P0] 由于k+1一定在[P0,P] 中,所以一定有S[K+1,P]=T[K+1-P0,P-P0] ,我们令len=next[K+1-P0] ,然后将T串的0号位置对准S的k+1位置. 根据next[]数组的定义,T[K+1-P0..K+1-P0+len-1]=T[0..len-1]
接下来就会有两种情况
情况一:
k+len<P
我们不难发现,S[k+len+1]!=T[len]是必然的,否则len作为最长的匹配就会产生矛盾.
所以,这种情况下extend[k+1] = len
情况二:
k+len>=P
也就是说虽然T的匹配到了len-1,但是实际上对于S来说,P(包含)之后的能否匹配成功是未知的,所以我们从S[p]开始尝试匹配.
模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
const int MAX=100010; //字符串长度最大值
int Next[MAX],extend[MAX];
//预处理计算Next数组
void getNext(char str[])
{
int i=0,j,po,len=strlen(str);
next[0]=len; //初始化next[0]
while(str[i]==str[i+1] && i+1<len) i++; next[1]=i; //计算next[1]
po=1; //初始化po的位置
for(i=2;i<len;i++)
{
if(next[i-po]+i < next[po]+po) //第一种情况,可以直接得到next[i]的值
next[i]=next[i-po];
else //第二种情况,要继续匹配才能得到next[i]的值
{
j = next[po]+po-i;
if(j<0) j=0; //如果i>po+next[po],则要从头开始匹配
while(i+j<len && str[j]==str[j+i]) j++; next[i]=j;
po=i; //更新po的位置
}
}
}
//计算extend数组
void EXKMP(char s1[],char s2[])
{
int i=0,j,po,len=strlen(s1),l2=strlen(s2);
getNext(s2); //计算子串的next数组
while(s1[i]==s2[i] && i<l2 && i<len) i++; extend[0]=i;
po=0; //初始化po的位置
for(i=1;i<len;i++)
{
if(next[i-po]+i < extend[po]+po) //第一种情况,直接可以得到extend[i]的值
ex[i]=next[i-po];
else //第二种情况,要继续匹配才能得到extend[i]的值
{
j = extend[po]+po-i;
if(j<0) j=0; //如果i>extend[po]+po则要从头开始匹配
while(i+j<len && j<l2 && s1[j+i]==s2[j]) j++; extend[i]=j;
po=i; //更新po的位置
}
}
}
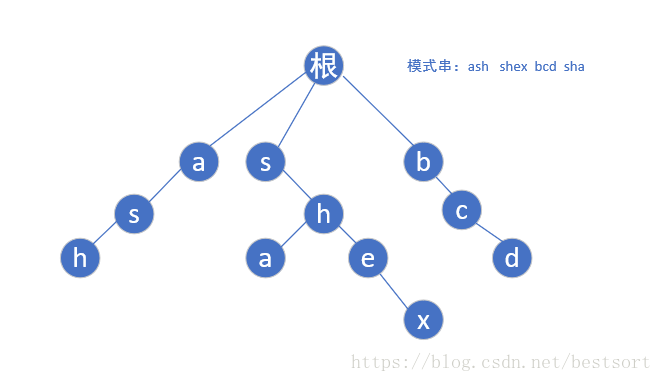
字典树
字典树在之前的博客中有提到了,此处不再赘述.
介绍
强调一下定义:字典树又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
字典树就是像平时使用的字典一样的,我们把所有的单词编排入一个字典里面,当我们查找单词的时候,我们首先看单词首字母,进入首字母所再的树枝,然后看第二个字母,再进入相应的树枝,假如该单词再字典树中存在,那么我们只用花费字典树就是像平时使用的字典一样的,我们把所有的单词编排入一个字典里面,当我们查找单词的时候,我们首先看单词首字母,进入首字母所再的树枝,然后看第二个字母,再进入相应的树枝,假如该单词再字典树中存在,那么我们只用花费单词长度的时间查询到这个单词。查询到这个单词。
AC自动机
介绍
AC自动机是一种多模式匹配的算法,其用于解决给出一个主串以及多个模式串,然后求匹配的问题.
AC自动机=字典树+Fail指针(KMP思想)
在字典树上,每个点的fail,指向的就是和这个节点所表示的串拥有最长公共后缀的节点
AC自动机的字符串插入和字典树完全相同 .我们在此仅讨论如何构建Fail指针
执行以下步骤(bfs):
-
每个模式串的首字母指向(无特殊说明就是Fail指针)根节点,将根节点的儿子加入队列
-
弹出队首结点P,遍历其儿子节点(就是
a~z26个字母)如果此儿子节点不存在,就将这个儿子节点的Fali指针指向根节点.
如果此儿子节点(c)存在,就将这个儿子节点指向((P节点指向的节点)的和c对应字母相同的儿子节点),然后将儿子节点加入队列.
上一条是在太绕了,用代码表示
fail[trie[now][i]] = trie[fail[now]][i]; -
反复执行,直到队列为空
模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include<algorithm>
#include<iostream>
#include<iterator>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#define ll long long
using namespace std;
const int maxn = 200;
//查询文本串中出现了多少模式串
struct trie {
int next[maxn][26], fail[maxn], end[maxn];
int root, cnt;
int new_node() {
memset(next[cnt], -1, sizeof next[cnt]);
end[cnt++] = 0;
return cnt - 1;
}
void init() {
cnt = 0;
root = new_node();
}
void insert(char *buf) {//字典树插入一个单词
int len = strlen(buf);
int now = root;
for (int i = 0; i < len; i++) {
int id = buf[i] - 'a';
if (next[now][id] == -1) { next[now][id] = new_node(); }
now = next[now][id];
}
end[now]++;
}
void
build() {//构建fail指针
queue<int> q;
fail[root] = root;
for (int i = 0; i < 26; i++) {
if (next[root][i] == -1) { next[root][i] = root; }
else {
fail[next[root][i]] = root;
q.push(next[root][i]);
}
}
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = 0; i < 26; i++) {
if (next[now][i] == -1) { next[now][i] = next[fail[now]][i]; }
else {
fail[next[now][i]] = next[fail[now]][i];
q.push(next[now][i]);
}
}
}
}
int query(char *buf) {
int len = strlen(buf);
int now = root;
int res = 0;
for (int i = 0;
i < len; i++) {
int id = buf[i] - 'a';
now = next[now][id];
int tmp = now;
while (tmp != root) { // 一开始这里不理解,事实上是沿着某一个路走,走一步,不仅看当前,还看其他的分支上会不会有和当前的结果匹配的情况.之后慢慢分析
if (end[tmp]) {
res += end[tmp];
end[tmp] = 0;
}
tmp = fail[tmp];
}
}
return res;
}
} ac;