CodeNote

「CodeNote」 二分图匹配

Posted by Dawn-K's Blog on October 7, 2019

二分图匹配

崔添翼

参考资料

参考资料2

介绍

二分图

二分图是一种图论的景点模型.二分图由两个点集U,V组成.点集内部不存在边,点集之间存在边.

匹配

给定一个二分图G,在G的一个子图M的点集E中,任何两个边不依附于同一个顶点,则称M是一个匹配.

特别地,如果无法通过增加未匹配的边来进一步增大匹配的边数,则称M为极大匹配.

极大匹配不唯一,他们中边数最多的那个称之为最大匹配.

如果一个图中,图中的每个点都和某个边相连,则称为完备匹配或完美匹配.(虽然没有确切的结论,但是博客上面说完备匹配指的是两个点集中较小的那个均有边,完美匹配是指的两个点集大小相同时的完备匹配)

**完备匹配: 匹配数=min( X , Y ), X 表示X部的点数， Y 表示Y部的点数**

匈牙利算法

二分图匹配的核心算法之一.

该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法,上界的时间复杂度O(n*m),,空间复杂度O(n+e). e表示边的个数

增广路

img

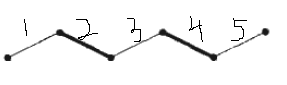
如果我们有形如图中的这种路径(粗线表示选中),我们会发现,如果将粗线和细线进行交换,依旧是一个匹配,而且匹配的数量一定加一.

我们就称这种路为增广路,匈牙利算法的核心就是不断的寻找增广路,直至没有.

算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

// 核心部分
// n表示左侧节点个数,m表示右侧节点个数
bool Find(int u, int dfn) {  // u 表示起点,寻找增广路,dfn表示时间戳,这样的写法可以减少对vis的反复初始化(那样会使得复杂度一定是O(n*m),这种写法则一般不会跑到上界)
    for (int i = head[u]; i + 1; i = edge[i].next) {
        int v = edge[i].v;
        if (vis[v] != dfn) { // 遇上了此轮已经经历过的节点,则无论当时成功与否,都不应该继续遍历了(成功加入匹配了,自然不能再加,加入匹配失败了,说明used[v]节点也找不到其他匹配)
            vis[v] = dfn;
            if (!used[v] || Find(used[v], dfn)) {
                used[v] = u;
                return true;
            }
        }
    }
    return false;
}
void work(){
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
        if (Find(i, i)) {
            ++ans;
        }
    }
    printf("%d\n", ans);
}

如何理解呢?

也就是说,我们先让当前节点u尝试匹配一个v(无论这个节点之前有没有被其他匹配过,都要尝试一下)

如果v之前没有被匹配过,则将u匹配v一定可以成功,增加一个匹配边,返回true

如果v之前被节点used[v]匹配过,则就让used[v]节点放弃v,然后让used[v]尝试去匹配其他节点,如果used[v]匹配其他节点(这是个递归过程)成功了,那么u就匹配v节点,如果失败了,u就去寻求其他节点.

如果最后u也没有匹配到其他节点,那么就范围false.

总体的算法就是枚举u,一个一个尝试增广路,最后统计答案.

模板(邻接表)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

// https://www.luogu.org/problem/P3386
#include <bits/stdc++.h>
#define ll long long
#define maxn 1010
#define maxm 1000000 + 100  // 切记,这里很容易写错,边的数量应当是n*m
using namespace std;
struct Egde {
    int u, v, next;
} edge[2 * maxm];
int cnt;
int head[maxn];
void add(int u, int v) {
    edge[cnt].u = u;
    edge[cnt].v = v;
    edge[cnt].next = head[u];
    head[u] = cnt;
    ++cnt;
}
int used[maxn], vis[maxn];
int k, m, n;
void init() {
    cnt = 0;
    for (int i = 1; i <= n; ++i) {
        head[i] = -1;
    }
    for (int i = 1; i <= m; ++i) {
        vis[i] = 0;
        used[i] = 0;
    }
}
bool Find(int u, int dfn) {  // u 表示起点,寻找增广路
    for (int i = head[u]; i + 1; i = edge[i].next) {
        int v = edge[i].v;
        if (vis[v] != dfn) {
            vis[v] = dfn;
            if (!used[v] || Find(used[v], dfn)) {
                used[v] = u;
                return true;
            }
        }
    }
    return false;
}

int main() {
    while (scanf("%d%d%d", &n, &m, &k) != EOF) {
        init();
        for (int i = 0; i < k; ++i) {
            int u, v;
            scanf("%d%d", &u, &v);
            if (v > m || u > n) { // 这个是洛谷模板题的数据坑点
                continue;
            }
            add(u, v);
        }
        int ans = 0;
        for (int i = 1; i <= n; ++i) {
            if (Find(i, i)) {
                ++ans;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}
/*
4 4 6
1 1
1 3
2 1
2 2
3 1
4 1
ans = 3
*/

模板(邻接矩阵)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

#include <bits/stdc++.h>
#define ll long long
#define maxn 1010
#define maxm int(1e6) + 100
using namespace std;
bool mp[maxn][maxn];
int n, m, k;
int used[maxn], vis[maxn];
bool Find(int u, int dfn) {
    for (int i = 1; i <= m; ++i) {
        if (mp[u][i]) {
            if (vis[i] != dfn) {
                vis[i] = dfn;
                if (!used[i] || Find(used[i], dfn)) {
                    used[i] = u;
                    return true;
                }
            }
        }
    }
    return false;
}

int match() {
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
        vis[i] = 0;
        used[i] = 0;
    }
    for (int i = 1; i <= n; ++i) {
        if (Find(i, i)) {
            ++ans;
        }
    }
    return ans;
}
int main() {
    while (scanf("%d%d%d", &n, &m, &k) != EOF) {
        for (int i = 0; i <= max(n, m); ++i) {
            for (int j = 0; j <= max(n, m); ++j) {
                mp[i][j] = 0;
            }
        }
        for (int i = 0; i < k; ++i) {
            int x, y;
            scanf("%d%d", &x, &y);
            mp[x][y] = 1;
        }
        printf("%d\n", match());
    }
    return 0;
}

带权二分图的最佳匹配(KM算法)

参考资料

如果二分图的每条边都有一个权（可以是负数），要求一种完备匹配方案，使得所有匹配边的权和最大，记做最佳匹配。（特殊的，当所有边的权为1时，就是最大完备匹配问题）

最佳匹配: 带权二分图的权值最大的完备匹配.

注意: 二分图的最佳匹配不一定是二分图的最大权匹配。

比如 x =2, y =2 x1->y1 x2->y1 x2->y2 ,假如第二条边权值很大,那么就发现最佳匹配和最大权匹配并不相同.

KM算法是对匈牙利算法的一种贪心扩展(然而匈牙利算法是后提出的).时间复杂度是O(n^3)

思路

生成子图:若图G的一个子图包含G的所有顶点(也就是可以去掉一些边)，称该子图为G的生成子图.

KM算法是这样:

定义lx[i]表示x集合中第i个点的点权,ly[i]表示y集合中第i个点的点权(点权具体的取值我们之后再说,学术一些叫可行顶点标号).我们令所有的边都满足

lx[u]+ly[v] >= G[u][v]

然后我们将所有边都满足lx[u]+ly[v] == G[u][v] 的生成子图称为相等子图.

相等子图有四个性质:

  1. 在任意时刻，相等子图上的最大权匹配一定小于等于相等子图的顶标和(因为根据定义,即使完美匹配也不会超过点权和)
  2. 在任意时刻，相等子图的顶标和即为所有顶点的顶标和(因为是生成子图,点都是相同的).
  3. 扩充相等子图后，相等子图的顶标和将会减小(这个稍后解释)
  4. 当相等子图的最大匹配为原图的完备匹配时，匹配边的权值和等于所有顶点的顶标和，此匹配即为最佳匹配。 (非常重要,也是KM算法的核心).

我们相当于以顶标和作为限制,然后将限制不断放宽,每次限制放宽,就会有新的节点加入,直至找到合法解,这个解就是最后的答案.

换句话说,只要我们不断扩充相等子图,在扩充的过程中一旦有一个相等子图拥有了完备匹配,此完备匹配就是原图的最佳匹配.

限制放宽的算法如下:

如果我们没有找到增广路径，则我们一定找到了许多条从Xi出发并结束于X部的匹配边与未匹配边交替出现的路径，姑且称之为交错树。我们将交错树中X部的顶点顶标减去一个值d，交错树中属于Y部的顶点顶标加上一个值d。这个d值就是交错树的边中顶标和与边权之差最小的边.

以下是简单证明:

  1. 两端都在交错树中的边，其顶标和没有变化。也就是说，它原来属于相等子图，现在仍属于相等子图。

  2. 两端都不在交错树中的边，其顶标也没有变化。也就是说，它原来属于（或不属于）相等子图，现在仍属于（或不属于）相等子图。

  3. X端不在交错树中，Y端在交错树中的边，它的顶标和会增大。它原来不属于相等子图，现在仍不属于相等子图。

  4. X端在交错树中，Y端不在交错树中的边,它的顶标和会减小。也就说，它原来不属于相等子图，现在可能进入了相等子图，因而使相等子图得到了扩大。

这四种情况保证了一定会有至少一个边加入相等子图.

当X部的所有顶点都找到了增广路径后，则找到了完备匹配(只要是完备的就可以,也就是反复套用匈牙利算法,直至x点集中的点全部找到对应的匹配点)，此完备匹配即为最佳匹配。

崔添翼:

保证对于每条边w[i][j]都有lx[i]+ly[j]-w[i][j]>=0。如果所有满足lx[i]+ly[j]==w[i][j]的边组成的导出子图中存在一个完美匹配，那么这个完美匹配肯定就是原图中的最大权匹配。理由很简单：这个匹配的权值之和恰等于所有顶标的和，由于上面的那个不等式，另外的任何匹配方案的权值和都不会大于所有顶标的和。

疑问: 会不会出现找不到的情况?如果原图就不存在完备匹配会发生什么?

模板

HDU2255

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94

// O(n^4)版本,主要用于理解
#include <bits/stdc++.h>
#define ll long long
#define maxn 350
#define INF 0x3f3f3f3f
#define maxm 1000000 + 100  // 切记,这里很容易写错,边的数量应当是n*m
using namespace std;

int G[maxn][maxn], lx[maxn], ly[maxn], used[maxn];
bool s[maxn], vis[maxn];
int k, m, n;
bool Find(int u) {  // u 表示起点,寻找增广路
    s[u] = 1;
    for (int j = 1; j <= n; ++j) {
        if (lx[u] + ly[j] == G[u][j] && !vis[j]) {
            vis[j] = 1;
            if (!used[j] || Find(used[j])) {
                used[j] = u;
                return true;
            }
        }
    }
    return false;
}
void update() {
    // 求出两点点权和 与 边权之差的最小值
    int a = INF;
    for (int i = 1; i <= n; ++i) {
        if (s[i]) {
            for (int j = 1; j <= n; ++j) {
                if (!vis[j]) {
                    a = min(a, lx[i] + ly[j] - G[i][j]);
                }
            }
        }
    }
    for (int i = 1; i <= n; ++i) {
        if (s[i]) {
            lx[i] -= a;
        }
        if (vis[i]) {
            ly[i] += a;
        }
    }
}
// 因为是完美匹配,所以两边的点的个数认为是相同的,都是n
ll km() {
    for (int i = 1; i <= n; ++i) {
        used[i] = lx[i] = ly[i] = 0;
        for (int j = 1; j <= n; ++j) {
            lx[i] = max(lx[i], G[i][j]);
        }
    }
    // 程序反复运行,直到找到完备匹配(x集合中的所有点都配对成功)
    for (int i = 1; i <= n; ++i) {
        while (1) {
            for (int j = 1; j <= n; ++j) {
                s[j] = vis[j] = 0;
            }
            if (Find(i)) {
                break;
            } else {
                update();
            }
        }
    }
    // 此处是枚举右端点,然后找已经匹配的边,统计答案
    ll ans = 0;
    for (int i = 1; i <= n; ++i) {
        if (used[i]) {
            ans += G[used[i]][i];
        }
    }
    return ans;
}

int main() {
    while (scanf("%d", &n) != EOF) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                G[i][j] = 0;
            }
        }
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                int w;
                scanf("%d", &w);
                G[i][j] = w;
            }
        }
        printf("%lld\n", km());
    }
    return 0;
}

上面的模板是O(n^4)的,有一些题目会卡,所以在经过查询之后,发现了这个算法还有个常见的优化,就是slack(松弛)优化.

参考资料3

这个优化的思路是这样的:通过前文我们发现,我们要找的边是x端在交错树上,而y端不在的.也就是在跑完匈牙利算法后,对于边(i,j),如果满足s[i]==1 vis[j]==0,那么它就是松弛的对象.

我们发现update()的作用就是用以找到这些边然后加以松弛,但是它最初的实现时暴力扫描所有边,实际上是非常低效的,所以我们就在运行匈牙利算法时,就从y节点的角度去记录对于yi,其相连的边中 min(点权和-边权),然后update的双重循环就被优化成了单重.也就是slack[j]表示右边的点j的所有不在导出子图的边对应的lx[i]+ly[j]-G[i][j]的最小值

另外要注意的时,在update修改点权的时候,要将所有的不在交错树上的y节点(也就是上文提到的节点)的slack值减去d.这是因为所有在交错树中的lx[i]减去了d.(slack的定义就是对于不在交错树上的y,其和所有在交错树上的x的(点权和-边权)的最小值,所以既然所有在交错树上的x都减去了d,那么Y中所有的不在交错树上的y的slack的值理应减少d).

这个循环据说是在完全图时有巨大优化.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99

// O(n^3)版本,但是不要抱太大希望,因为在HDU2255上,它甚至比O(n^4)的算法还要慢50ms,可以作为上个算法被卡时的思路
#include <bits/stdc++.h>
#define ll long long
#define maxn 350
#define INF 0x3f3f3f3f
#define maxm 1000000 + 100  // 切记,这里很容易写错,边的数量应当是n*m
using namespace std;

int G[maxn][maxn], lx[maxn], ly[maxn], used[maxn], slack[maxn];
bool s[maxn], vis[maxn];
int k, m, n;
bool Find(int u) {  // u 表示起点,寻找增广路
    s[u] = 1;
    for (int j = 1; j <= n; ++j) {
        if (vis[j])
            continue;
        int gap = lx[u] + ly[j] - G[u][j];
        if (gap == 0) {
            vis[j] = 1;
            if (!used[j] || Find(used[j])) {
                used[j] = u;
                return true;
            }
        } else {
            slack[j] = min(slack[j], gap);
        }
    }
    return false;
}
void update() {
    // 求出两点点权和 与 边权之差的最小值
    int d = INF;
    for (int j = 1; j <= n; ++j) {
        if (!vis[j]) {
            d = min(d, slack[j]);
        }
    }
    for (int i = 1; i <= n; ++i) {
        if (s[i]) {
            lx[i] -= d;
        }
        if (vis[i]) {
            ly[i] += d;
        } else {
            slack[i] -= d;
        }
    }
}
// 因为是完美匹配,所以两边的点的个数认为是相同的,都是n
ll km() {
    for (int i = 1; i <= n; ++i) {
        used[i] = lx[i] = ly[i] = 0;
        for (int j = 1; j <= n; ++j) {
            lx[i] = max(lx[i], G[i][j]);
        }
    }
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            slack[j] = INF;
        }
        while (1) {
            for (int j = 1; j <= n; ++j) {
                s[j] = vis[j] = 0;
            }
            if (Find(i)) {
                break;
            } else {
                update();
            }
        }
    }
    // 此处是枚举右端点,然后找已经匹配的边,统计答案
    ll ans = 0;
    for (int i = 1; i <= n; ++i) {
        if (used[i]) {
            ans += G[used[i]][i];
        }
    }
    return ans;
}

int main() {
    while (scanf("%d", &n) != EOF) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                G[i][j] = 0;
            }
        }
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                int w;
                scanf("%d", &w);
                G[i][j] = w;
            }
        }
        printf("%lld\n", km());
    }
    return 0;
}

// TODO: 更新最小权值的写法

CATALOG
    FEATURED TAGS
    CodeNote Web开发 软件工程 SpringBoot 互联网架构 垃圾回收的算法和实现 设计模式 android DAO 数据库 Python Vue Linux Unity VSCode学习 操作系统 版本控制 C++ View Java Kotlin Missing-Semester
    FRIENDS